Криптография: что это такое и зоны применения

Криптография или криптология, наука и искусство передачи сообщений в таком виде, чтобы их нельзя было прочитать без специального секретного ключа. В отечественном словоупотреблении термин «криптология» объединяет в себе «криптографию», т.е. шифрование сообщений, и «криптоанализ», т.е. несанкционированное расшифровывание сообщений (также широко употребляются термины «дешифровка / взламывание / ломка / взлом(ка) / вскрытие / раскрытие / раскалывание»). Слово «криптограф» происходит от древнегреческих слов kryptos ‘секрет’ и graphos ‘писание’. Исходное сообщение называется в криптографии открытым текстом, или клером. Засекреченное (зашифрованное) сообщение называется шифротекстом, или шифрограммой, или криптограммой. Процедура шифрования обычно включает в себя использование определенного алгоритма и ключа. Алгоритм – это определенный способ засекречивания сообщения, например компьютерная программа или, скажем, список инструкций. Ключ же конкретизирует процедуру засекречивания.

Криптография – системы шифрования

Пусть требуется зашифровать следующее сообщение (открытый текст):

DEAR DAD

SEND MORE MONEY AS SOON AS POSSIBLE TOM

«Дорогой папа. Как можно скорее пришли еще денег. Том.»

Один из способов шифрования простая замена, при которой каждая буква открытого текста заменяется на какую-то букву алфавита (возможно, на ту же самую). Для этого отправитель сообщения должен знать, на какую букву в шифротексте следует заменить каждую букву открытого текста. Часто это делается путем сведения нужных соответствий букв в виде двух алфавитов, например так, как показано ниже в таблице:

Алфавит ОткрытыйABCDEFGHIJKLMNOPQRSTUVWXYZШифровальныйBLUESTOCKINGADFHJMPQRVWXYZ

Шифрограмма получается путем замены каждой буквы открытого текста на записанную непосредственно под ней букву шифровального алфавита.

ESBM EBE

HGSBPS PSDE AFMS AFDSY BP PFFD BP HFPPKLGS QFA

Две алфавитные последовательности, используемые в процессе шифрования, называются, соответственно, открытым и шифровальным компонентом системы. Чтобы получатель шифрограммы мог восстановить открытый текст и прочитать сообщение, ему необходимо иметь копию вышеприведенной таблицы. Дешифровщик повторяет в обратном порядке все действия шифровальщика, раскрывая тем самым содержание сообщения.

В вышеприведенном примере использовался алгоритм побуквенной замены. Этот метод называется простой, или моноалфавитной заменой. Ключ к данному шифру состоит из таблицы, содержащей открытый и шифровальный алфавиты, в которой указывается, на какую букву в шифротексте следует заменить букву открытого текста. В такой криптографической системе предполагается, что алгоритм шифрования общеизвестен, тогда как ключ доступен только отправителю и получателю соответствующих сообщений.

В открытом алфавите буквы расположены в их обычной последовательности; такой алфавит называется прямой стандартной последовательностью. Шифровальный же алфавит в нашем примере состоит из 26 букв латинского алфавита, определенным образом переставленных с использованием ключевого слова BLUESTOCKING (букв. «синий чулок»). После ключевого слова (ключевой фразы) ключ далее записывается с опущением всех тех букв, что уже появились в этом слове (или в первом слове этой фразы), а затем вписываются остающиеся буквы алфавита в обычном порядке, опять же с опущением всех ранее появившихся букв. Так, если в качестве ключевой мы используем фразу UNITED STATES OF AMERICA, то шифровальный алфавит будет выглядеть следующим образом:

U N I T E D S A O F M R C B G H J K L P Q V W X Y Z

С помощью ключевого слова (фразы) при шифровании можно перемешать любую алфавитную последовательность. Использование ключевых слов облегчает восстановление открытого и шифровального компонента системы, поскольку при этом необходимо запомнить только соответствующее ключевое слово (фразу). Нет необходимости записывать (или разгадывать) какие бы то ни было таблицы: если помнить ключевое слово, то алфавитную последовательность всегда можно восстановить по памяти.

В вышеприведенной шифрограмме между словами сохранены пробелы, однако шифровку можно сделать более защищенной (или, как говорят криптографы, устойчивой, или стойкой ко взлому; шифр считается тем более стойким, чем дольше он не поддается вскрытию) путем удаления межсловных пробелов из окончательного шифротекста. Согласно установившейся практике, шифротекст принято делить на группы из пяти букв каждая. (Когда-то телеграфные компании при взимании платы каждую группу из пяти букв считали как одно слово открытого текста.) Если убрать пробелы между словами, то нашу шифрограмму можно было бы записать так:

ESBME BEMGS BPSPS DEAFM SAFDS YBPPF FDBPH FPPKL GSQFA

Замена – одно из основных криптографических преобразований. Другим важнейшим шифровальным алгоритмом является перестановка. В шифре перестановки все буквы открытого текста остаются без изменений, но переставляются согласно заранее оговоренному правилу. Здесь также может использоваться ключ, управляющий процедурой шифрования. Так, используя в качестве ключа слово PANAMA, мы могли бы зашифровать вышеупомянутый открытый текст следующим образом:

КлючP A N A M AЧисловая последовательность6 1 5 2 4 3Блок перестановкиD E A R D A D P L E A S E S E N D M O N E Y A S S O O N A S P O S S I B L E T O MШифрограммаEPSNO OEREN YNSOA SMSSB DADAA IMALE EOSTD DEOSP L

В этом примере ключевое слово использовано для получения шифровальной числовой последовательности путем нумерации букв ключевого слова (относительно друг друга) в порядке их следования слева направо в стандартном алфавите. Далее под числовой последовательностью в строках, равных по длине ключевому слову, записан открытый текст. В процессе шифрования текст выписывается уже по отдельным столбцам в порядке, определяемом данной числовой последовательностью. Этот метод перестановки называется перестановкой столбцов, но можно избрать и другие «маршруты» перестановки, например выписывать шифротекст следуя по диагонали (слева направо или справа налево, или же чередуя левое и правое направления) или по спирали и т.п. Кроме того, буквы шифротекста могут записываться в виде различных геометрических фигур или любыми другими способами. Один из них состоит в двойном шифровании путем повторной перестановки столбцов. При этом и в первом, и во втором блоках перестановки может быть использовано одно и то же ключевое слово, хотя лучше использовать разные ключевые слова. Такой шифр, называющийся двойной перестановкой, получил широкое распространение в 20 в.

Третьим основным алгоритмом шифрования является дробление. При этом каждой букве открытого текста сопоставляется более одного символа шифротекста, после чего символы перемешиваются (переставляются) в определенном порядке. Ниже приведена система, демонстрирующая процедуру дробления с использованием знаменитого шифра Bifid, авторство которого приписывается французскому криптографу Феликсу Мари Деластеллю.

Ключевая фразаUNITED STATES OF AMERICA 1 2 3 4 5 1 U N I T EПолибианский квадрат2 D S A O F 3 M R C B G 4 H K L P Q 5 V W X Y ZОткрытый текстDEARDADPLEASESENDMOREMONEYСоответствующая строка21232224412212112323132115Соответствующий столбец15321314353252521142514254ШифротекстDASOHSNUAAIDEERITGRWWUKVKY

Сначала составляется шифровальная таблица размером 5ґ5 (т.н. полибианский квадрат), куда построчно вписывается шифровальный алфавит с ключевой фразой UNITED STATES OF AMERICA; причем ради того, чтобы общее число букв алфавита не превышало 25, буква J опускается (поскольку эта буква, с одной стороны, малоупотребительна в английских текстах, а с другой – вполне может быть заменена буквой I, без какого-либо урона для смысла). В данной таблице букве A, например, соответствуют координаты 23, букве B – 34 и т.д.

Далее, в процессе шифрования под каждой буквой открытого текста в столбик записываются ее табличные координаты – номер строки и, ниже, номер столбца, а затем получившаяся цифровая последовательность переводится с помощью той же таблицы обратно в буквенную форму, но на этот раз она читается уже в строчку, т.е. 21 – буква D, 23 – буква A, 22 – буква S и т.д. При таком шифровании координата строки и координата столбца каждой буквы оказываются разъединенными, что характерно именно для раздробляющего шифра.

Замена, перестановка и дробление представляют собой основные криптографические алгоритмы. Эти три базовых преобразования, зачастую в сочетании друг с другом, используются в большинстве систем шифрования для создания очень сложных шифровальных алгоритмов, особенно когда шифрование производится компьютером.

Код отличается от шифра тем, что подходит к преобразованию открытого текста скорее с лингвистической точки зрения, нежели с чисто формальной, как в вышеописанных примерах. (В повседневном употреблении термин «код» обыкновенно путают с термином «шифр».) Кодирование, как правило, включает в себя применение пространной таблицы или кодового словаря, где перечислены числовые соответствия (эквиваленты) не только для отдельных букв, но и для целых слов и наиболее употребительных фраз и предложений. Например, такая кодовая группа, как AABRT, вполне может соответствовать открытому тексту «как можно быстрее». Раньше в дипломатических и военных криптографических системах часто использовались весьма пространные коды. Однако с появлением компьютеров наибольшее распространение получили шифры.

Другие криптографические системы.

Криптография включает в себя и системы тайнописи, отличные от вышеописанных. Для сокрытия исходного сообщения могут использоваться симпатические (невидимые) чернила. Секретные сообщения могут содержаться в нотной партитуре в виде особой записи отдельных нот, а также мелодических и гармонических секвенций. В фотографии для сокрытия сообщения применяется метод микроскопических точек. Сообщение может быть также спрятано в рисунке, чертеже или картине.

Криптография – история

Ранняя история криптографии.

Как только возникло письмо, появились и способы его шифрования. В древних цивилизациях мы находим два вида письма: иератическое, или священное письмо, использовавшееся священнослужителями для тайного общения друг с другом, и демотическое письмо, употреблявшееся всеми остальными. И у греков, и у римлян, и у других сопоставимых с ними по историческому значению народов были свои системы тайного письма. Изобретение первой системы скорописи, которая изначально замышлялась как секретное письмо, приписывается Туллиусу Тиро, вольноотпущенному рабу Цицерона (106–43 до н.э.).

Но только в период позднего Средневековья криптография превратилась в важный фактор дипломатических, торговых и военных сношений. По мере формирования европейских наций-государств возрастала нужда в средствах секретной коммуникации, особенно в сфере дипломатии. Со временем, когда отношения между новыми политическими образованиями установились, каждое государство учредило свою «тайную палату», в чьи функции входили перехват, досмотр и вскрытие шифров и кодов соседних государств. Зачастую это было сопряжено также с подделкой соответствующих документов и печатей. Так родилась наука криптоанализа, более известная под названием «взламывание шифров».

Первая книга по криптографии, называвшаяся Polygraphiae Libri Sex, была написана в 1499 Иоганном Трисемусом, аббатом бенедиктинского монастыря Св. Мартина в Шпанхейме (Германия). Хотя труд Трисемуса был весь пронизан кабалистическими и оккультными аллюзиями, в этой рукописи были описаны многие шифры – как широко бытовавшие в то время, так и изобретенные самим автором. Эта работа была чрезвычайно популярна, первое латинское издание появилось в 1518, а в 1541 книга была переиздана на французском языке. Вскоре последовал и ее перевод на немецкий язык. Книга вызвала гнев многих монарших дворов Европы, полагавших, что Трисемус выдал в ней слишком много секретов, и автор едва избежал сожжения на костре.

В 1550 итальянец Джироламо Кардано опубликовал книгу De subtilitate libri xxi. Кардано изобрел шифр, называемый решеткой, или трафаретом, в котором секретное послание оказывалось сокрыто внутри более длинного и совершенно невинно выглядевшего открытого текста. Секретное сообщение можно было обнаружить, наложив на открытый текст лист пергаментной бумаги с прорезями (трафарет). Cлова, появлявшиеся в прорезях, и составляли секретное послание.

Примерно в то же время о шифрах писал Джамбаттиста делла Порта. Труд Порта был скопирован и слегка переделан французским дипломатом Блезом де Виженером, труд которого Traité des chiffres приобрел широкую известность.

Для периода примерно с 16 по 19 вв. типичным был т.н. номенклатор – шифр, представлявший собой сочетание шифра замены и небольшого кода. Номенклатор обычно содержал кодовые эквиваленты букв алфавита и наиболее употребительных слогов, слов и словосочетаний, а также ряд специальных символов. Чаще всего в нем встречались специально созданные для этой цели символы, но нередко также использовалась астрологическая и оккультная символика.

Номенклатор был разработан как система шифрования, наилучшим образом приспособленная к наиболее употребительным в то время методам криптоанализа, которые, как правило, включали подсчет частоты появления в тексте каждого шифрового символа и поиск в тексте слов и выражений, содержащих характерные для данного языка сочетания букв. Метод частотного анализа букв основан на том, что в любом языке одни буквы встречаются чаще, чем другие. В английском языке, например, чаще других встречается буква Е. Другие наиболее часто встречающиеся буквы – T, A, O, N, R и S. (Целиком эту группу букв легко запомнить в виде слова «SENORITA».) А буквы J, K, X и Z встречаются в английском редко. Поскольку в ходе операции замены частота буквы не меняется, ключ к разгадке истинного значения того или иного шифросимвола заключается иногда в подсчете частоты его появления в шифротексте. Равным образом операция простой замены не вносит изменений и в сочетания букв (буквенные модели). Например, слово ATTACK, будучи зашифрованным, может принять вид XJJXBU. Несмотря на то, что значения букв при этом изменились, буквенная модель слова (а именно две одинаковых буквы, обрамленные слева и справа одной и той же буквой, после чего следуют две другие различные буквы) осталась неизменной.

Чтобы усложнить частотный анализ букв, каждую букву клера стали заменять двумя и более шифросимволами. Такая операция обычно разрушала и буквенные модели, от наличия которых в значительной мере зависел успех криптоанализа. Рассмотрим в качестве иллюстрации, т.н. «малый шифр», использовавшийся в наполеоновской армии для связи между войсками и генеральным штабом.

A-15 AR-25 AL-39M-114 MA-107B-37 BU-3 BO-35 BI-29N-115 NE-94 NI-116C-6 CA-32 CE-20O-90 OT-153D-23 DE-52P-137 PO-152E-53 ES-82 ET-50 EN-68Q-173 QUE-136F-55 FA-69 FE-58 FO-71R-169 RA-146 RE-126 RI-148G-81 GA-51S-167 SA-171 SE-177 SI-134H-85 HI-77SO-168 SU-174I-119 IS-122T-176 TI-145 TO-157J-87 JAI-123U-138K-?V-164 VE-132 VI-161 VO-175L-96 LU-103 LE-117W, X, Y-?LA-106Z-166

Приведенная выше таблица замены была дешифрована французским криптографом Этьеном Базери. В имевшихся в его распоряжении шифровках некоторые буквы клера (K, W, X и Y) не встречались, поэтому он не смог определить их шифровых эквивалентов.

«Малый шифр» содержит числовые эквиваленты для всех букв алфавита, а также для часто встречающихся биграмм (двухбуквенных сочетаний) и некоторых триграмм (трехбуквенных сочетаний). С помощью этого шифра, который специалисты называют силлабарием (слоговым алфавитом), слово NAPOLEON «Наполеон», например, может быть зашифровано по-разному:

NAPOLEON1151513790965390115илиNAPOLEON1151515211790115

Использование подобных приемов сильно усложняет задачу криптоаналитика. Хотя наполеоновский шифр относительно невелик, в эпоху номенклаторов нередки были также криптосистемы, содержавшие сотни соответствий.

Криптография – наше время

С 1990-х годов страны начали в открытую формировать свои стандарты криптографических протоколов. США, к примеру, приняло в качестве стандарта для криптографии с закрытым ключом шифр Rijndael, более известный, как AES, в Европе приняли шифр NESSIE, в Японии — CRYPTREC.

Сами же алгоритмы сильно усложнились с точки зрения математических конструкций — чтобы затруднить криптоанализ (как линейный, так и на основе дифференциальных вычислений). Принципы выбора алгоритмов постепенно начали усложняться из-за новых требований, которые часто не связаны с математикой напрямую: например, из-за требований к устойчивости к атакам через сторонние каналы и посредством социальной инженерии.

«Также появляются совершенно новые направления в криптографии: на стыке математики и квантовых вычислений. Хотя у людей пока нет мощных квантовых компьютеров, уже разрабатываются способы взлома современных систем — в их числе алгоритм Шора. Но, используя технологии квантовых компьютеров, можно построить более надежные и совершенно новые механизмы передачи информации. Их разработка ведется с 1980-х годов», — рассказывает эксперт.

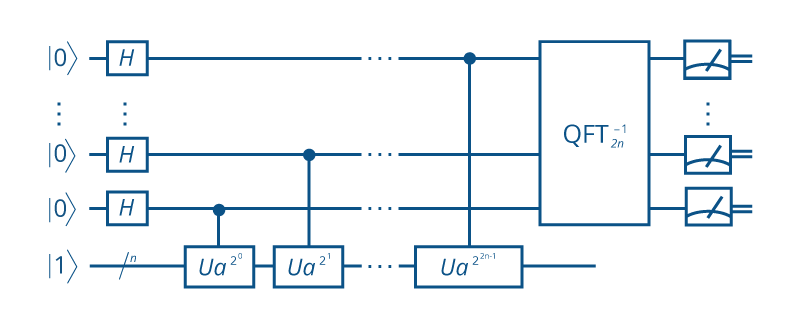
Квантовый алгоритм разложения числа на простые множители, который разработал Питер Шор. Алгоритм важен для задач квантовой криптографии: разложение натуральных чисел на множители используется при считывании банковских пластиковых карт и для других конфиденциальных операций. Нахождение способа дешифровки может обезоружить системы защиты

Компьютеризация и появление доступного интернета вывели криптографию в массы. Криптографические методы стали широко использовать бизнес и частные лица в электронных коммерческих операциях, телекоммуникациях и других сферах. Это привело к появлению новой валюты, которую не контролируют государства, — биткойн. И технологии, без которой не смогли бы проходить транзакции в криптовалютах, — блокчейн.

Сейчас криптография используется повсеместно. Кроме очевидного направления — передачи информации — это цифровое телевидение, сотовая связь, wi-fi, считывание билетов в транспорте, защита электронной почты от спама, банковские операции. Одно из новейших направлений — маркировка товаров для борьбы с подделками.

Именно оно является одной из самых важных задач для развития российской экономики. Ведь в 2015 году доля нелегального товарооборота достигала 9% рынка, то есть, фактически каждый десятый товар был подделкой. В абсолютных цифрах их стоимость достигала 2,5 триллионов рублей. Среди самых подделываемых товаров оказались одежда, обувь и алкоголь. На рынке минеральных вод доля нелегальных товаров достигла 20-25% в среднем и до 60% по отдельным позициям, подделывается 25% молочной продукции, каждый пятый флакон духов и каждая десятая пачка сигарет.

В 2018 году выявлено в 1,6 раза больше контрафакта, чем в 2017-м. Для того, чтобы обелить рынок было принято решение о создании единой системы цифровой маркировки и прослеживания товаров «Честный ЗНАК», которую реализуют Ростех и «Центр развития перспективных технологий».

Задача такой системы лежит как раз в плоскости криптографии. На упаковках товаров печатают Data Matrix-коды, которые состоят из двух частей: кода идентификации и криптохвоста. Коды генерирует система цифровой маркировки, в них зашифрована уникальная информация о товаре. Код идентификации определяет позицию товара в системе и едином каталоге, криптохвосты дополнительно шифруют каждый код на производстве. Из-за того, что система маркировки не хранит коды целиком, подделать их невозможно. Серию уникальных кодов нельзя и предсказать, а сам цифровой код не повторяется минимально в течение пяти лет с момента выпуска товарной позиции.

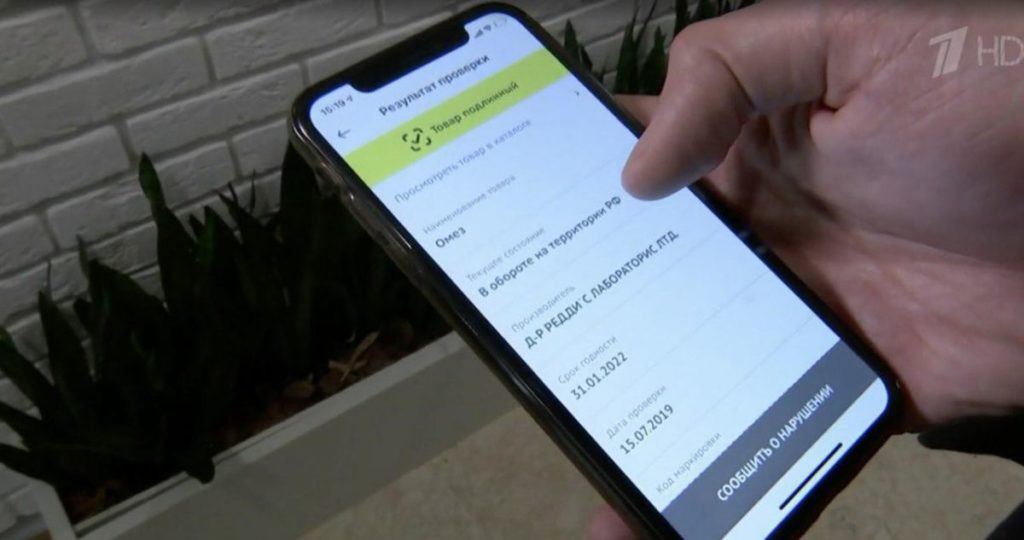
Одно из главных применений маркировки товаров. Покупатель может проверить, что товар в его руках — не подделка. Через приложение на смартфоне он считывает Data Matrix-код: если товар определился в системе, значит его произвели легально / ©Первый канал

Сейчас маркировка применяется в нескольких отраслях в добровольном режиме, обязательной же маркировке подлежат духи, шины, обувь, табак, фототехника и пять групп изделий легкой промышленности. С 1 января 2020 года стартует маркировка лекарств, в марте — молочной продукции.

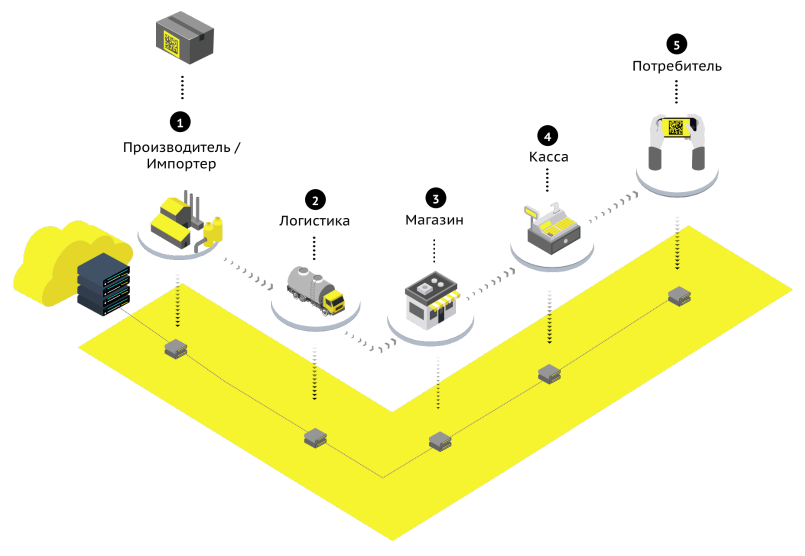
Система маркировки позволяет отследить движение товара на протяжении всего жизненного цикла: выход с конвейера, отгрузка поставщику, передача в розничный магазин, включая проверку кода в магазине, когда товар попадает на полку. Это исключает возможность вбросить подделку в число легальных товаров / ©Честный ЗНАК

«Развитие компьютерных технологий революционно изменило принципы построения криптосистем. Криптография ушла далеко вперед от примитивных шифров к сложным алгоритмам шифрования. А появление мобильной связи, интернета и смартфонов вывело криптографию в гражданское поле.

Криптография: алгоритмы шифрования

На сегодняшний день существует масса алгоритмов шифрования, имеющих значительную стойкость перед криптоанализом (криптографическую стойкость). Принято деление алгоритмов шифрования на три группы:

• Симметричные алгоритмы
• Ассиметричные алгоритмы
• Алгоритмы хэш-функций

Симметричные алгоритмы

Симметричное шифрование предусматривает использование одного и того же ключа и для зашифрования, и для расшифрования. К симметричным алгоритмам применяются два основных требования: полная утрата всех статистических закономерностей в объекте шифрования и отсутствие линейности.
Принято разделять симметричные системы на блочные и поточные.

В блочных системах происходит разбиение исходных данных на блоки с последующим преобразованием с помощью ключа.

В поточных системах вырабатывается некая последовательность (выходная гамма), которая в последующем накладывается на само сообщение, и шифрование данных происходит потоком по мере генерирования гаммы.

Обычно при симметричном шифровании используется сложная и многоступенчатая комбинация подстановок и перестановок исходных данных, причем ступеней (проходов) может быть множество, при этом каждой из них должен соответствовать «ключ прохода»

Операция подстановки выполняет первое требование, предъявляемое к симметричному шифру, избавляясь от любых статистических данных путем перемешивания битов сообщения по определенному заданному закону. Перестановка необходима для выполнения второго требования – придания алгоритму нелинейности. Достигается это за счет замены определенной части сообщения заданного объема на стандартное значение путем обращения к исходному массиву.

Симметричные системы имеют как свои преимущества, так и недостатки перед асимметричными.

К преимуществам симметричных шифров относят высокую скорость шифрования, меньшую необходимую длину ключа при аналогичной стойкости, большую изученность и простоту реализации.
Недостатками симметричных алгоритмов считают в первую очередь сложность обмена ключами ввиду большой вероятности нарушения секретности ключа при обмене, который необходим, и сложность управления ключами в большой сети.

Примеры симметричных шифров

• ГОСТ 28147-89 — отечественный стандарт шифрования
• 3DES (Triple-DES, тройной DES)
• RC6 (Шифр Ривеста )
• Twofish
• SEED – корейский стандарт шифрования
• Camellia – японский стандарт шифрования
• CAST (по инициалам разработчиков Carlisle Adams и Stafford Tavares)
• IDEA
• XTEA – наиболее простой в реализации алгоритм
• AES – американский стандарт шифрования
• DES – стандарт шифрования данных в США до AES

Асимметричные алгоритмы

Ассиметричные системы также называют криптосистемами с открытым ключом. Это такой способ шифрования данных, при котором открытый ключ передается по открытому каналу (не скрывается) и используется для проверки электронной подписи и для шифрования данных. Для дешифровки же и создания электронной подписи используется второй ключ, секретный.

Само устройство асимметричных криптосистем использует идею односторонних функций ƒ(х), в которых несложно найти х, зная значение самой функции но почти невозможно найти саму ƒ(х), зная только значение х. Примером такой функции может служить телефонный справочник большого города, в котором легко найти номер человека, зная его фамилию и инициалы, но крайне сложно, зная номер, вычислить владельца.

Принцип работы асимметричных систем

Допустим, имеются два абонента: А и В, и абонент В хочет отправить шифрованное сообщение абоненту А. Он зашифровывает сообщение с помощью открытого ключа и передает его уже зашифрованным по открытому каналу связи. Получив сообщение, абонент А подвергает его расшифрованию с помощью секретного ключа и читает.

Здесь необходимо сделать уточнение. При получении сообщения абонент А должен аутентифицировать свою личность перед абонентом В для того, чтобы недоброжелатель не смог выдать себя за абонента А и подменить его открытый ключ своим.

Примеры асимметричных шрифтов

• RSA (Rivest-Shamir-Adleman, Ривест — Шамир — Адлеман)
• DSA (Digital Signature Algorithm)
• Elgamal (Шифросистема Эль-Гамаля)
• Diffie-Hellman (Обмен ключами Диффи — Хелмана)
• ECC (Elliptic Curve Cryptography, криптография эллиптической кривой)
• ГОСТ Р 34.10-2001
• Rabin
• Luc
• McEliece

Криптография – Хеш-функции

Хешированием (от англ. hash) называется преобразование исходного информационного массива произвольной длины в битовую строку фиксированной длины.

Алгоритмов хеш-функций немало, а различаются они своими характеристиками – криптостойкостью, разрядностью, вычислительной сложностью и т.д.

Нас интересуют криптографически стойкие хеш-функции. К таким обычно предъявляют два требования:

• Для заданного сообщения С практически невозможно подобрать другое сообщение С’ с таким же хешем
• Практически невозможно подобрать пар сообщений (СС’), имеющих одинаковый хеш.

Требования называются стойкостью к коллизиям первого рода и второго рода соответственно.
Для таких функций остается важным и другое требование: при незначительном изменении аргумента должно происходить значительное изменение самой функции. Таким образом, значение хеша не должно давать информации даже об отдельных битах аргумента.

Примеры хеш-алгоритмов

• Adler-32
• CRC
• SHA-1
• SHA-2 (SHA-224, SHA-256, SHA-384, SHA-512)
• HAVAL
• MD2
• MD4
• MD5
• N-Hash
  • RIPEMD-160
• RIPEMD-256
• RIPEMD-320
• Skein
• Snefru
• Tiger (TTH)
• Whirlpool
• ГОСТ Р34.11-94 (ГОСТ 34.311-95)
• IP Internet Checksum (RFC 1071)

Криптографические примитивы

Для придания зашифрованной информации большей криптографической стойкости, в криптографической системе могут многократно применяться относительно простые преобразования – примитивы. В качестве примитивов могут использоваться подстановки, перестановки, циклический сдвиг или гаммирование.

Квантовая криптография

Квантовая криптография по праву считается новым витком в эволюции информационной защиты. Именно она позволяет создать практически абсолютную защиту шифрованных данных от взлома. Идея использовать квантовые объекты для защиты информации от подделки и несанкционированного доступа впервые была высказана Стефаном Вейснером в 1970 г. Спустя 10 лет ученые Беннет и Брассард, которые были знакомы с работой Вейснера, предложили использовать квантовые объекты для передачи секретного ключа. Читать статью “Квантовая криптография (шифрование)”

Криптография в цифровых технологиях

Криптография в цифровых технологиях необходима как инструмент защиты конфиденциальных данных а так же как средство противодействия незаконному копированию и распространению данных, являющихся интеллектуальной собственностью. Читать статью “Криптография в цифровых технологиях”

Квантовая криптография: что это такое?

Максимальная длина канала связи,позволяющего использовать метод квантовой криптографии,составляет всего лишь чуть больше сотни километров. Ученые из Российского квантового центра разработали способ значительно увеличить эту дистанцию. Представьте себе, что прежде чем отправить электронное письмо приятелю, вы должны достать карту, измерить расстояние до города, где он живет, и если окажется, что это расстояние больше, чем 100 км, вы со вздохом берете карандаш и бумагу и беретесь за обычное «бумажное» письмо — электронная почта дальше, чем на 100 км, не ходит.

Абсурдная ситуация? Но именно так сейчас обстоят дела с передачей квантовых данных по оптоволоконным линиям связи — рекордная дальность передачи здесь до сих пор лишь немного превышает сотню километров, а устойчивая работа на нормальных, не рекордных линиях вообще ограничивается 40 км. Это означает, например, что линию квантовой коммуникации можно организовать внутри Москвы, а вот о передаче данных в Петербург пока нечего и думать. Каковы же перспективы квантовой криптографии в области дальней связи?

Вскрытие на слух

Первый успешный эксперимент по квантовой передаче данных был проведен Беннетом и Жилем Брассаром в конце октября 1989 года, когда защищенная квантовая связь была установлена на расстоянии 32,5 см. Установка меняла поляризацию фотонов, но при этом блок питания шумел по‑разному в зависимости от того, какой была поляризация. Таким образом, окружающие могли свободно различать нули и единицы на слух. Как пишет Брассар, «наш прототип был защищен от любого подслушивающего, который оказался бы глухим». В октябре 2007 года методы квантовой криптографии были впервые применены в широкомасштабном проекте. Система квантовой защищенной связи, разработанная швейцарской компанией Id Quantique, использовалась для передачи данных о результатах голосования на парламентских выборах в швейцарском кантоне Женева. Таким образом, голоса швейцарцев были защищены как никакая другая информация.

Банкноты и блокноты

История квантовой криптографии началась еще в конце 1960-х годов, когда студент Колумбийского университета Стивен Визнер изложил своему бывшему сокурснику Чарльзу Беннету идею квантовых банкнот, которые в принципе нельзя подделать, поскольку это исключают законы природы. Суть идеи состояла в том, чтобы поместить на каждую банкноту несколько квантовых объектов. Это могут быть, например, ловушки с фотонами, каждый из которых поляризован под определенным углом в одном из двух базисов — либо под углом 0 и 90, либо 45 и 135 градусов. Серийный номер напечатан на банкноте, но соответствующая номеру комбинация поляризаций и базисов (фильтров, с помощью которых фотону придается или измеряется его поляризация) при этом известна только банку. Чтобы подделать такую банкноту, фальшивомонетчик должен измерить поляризацию каждого фотона, но он не знает, в каком базисе поляризован каждый из них. Если он ошибется с базисом, то поляризация фотона изменится, и поддельная банкнота будет с неверной поляризацией. Квантовые деньги до сих пор не появились, поскольку пока не удалось создать достаточно надежных ловушек для фотонов. Однако тогда же Визнер предложил использовать тот же самый принцип для защиты информации, и эта технология сейчас уже близка к реализации.

Первый протоколПервый протокол квантового распределения ключей был создан Жилем Брассаром и Чарльзом Беннетом в 1984 году и получил название BB84. Для передачи данных используются фотоны, поляризованные в четырех разных направлениях, в двух базисах — под углом 0 и 90 градусов (обозначается знаком +) либо 45 и 135 градусов (x). Отправитель сообщения A (традиционно его называют «Алиса») поляризует каждый фотон в случайно выбранном базисе, а затем отправляет его получателю B — «Бобу». Боб измеряет каждый фотон, тоже в случайно выбранном базисе. После этого Алиса по открытому каналу сообщает Бобу последовательность своих базисов, и Боб отбрасывает неправильные (не совпавшие) базисы и сообщает Алисе, какие данные «не прошли». При этом сами значения, полученные в результате измерений, они по открытому каналу не обсуждают. Если шпион (его обычно называют «Евой», от английского eavesdropping — подслушивание) захочет перехватить секретный ключ, он должен будет измерять поляризацию фотонов. Поскольку он не знает базиса, он должен будет определять его случайным образом. Если базис будет определен неправильно, то Ева не получит верных данных, а кроме того, изменит поляризацию фотона. Появившиеся ошибки сразу обнаружат и Алиса, и Боб.

Идеи Визнера, однако, были признаны далеко не сразу. Еще в начале 1970-х годов Визнер отправил свою статью о квантовой криптографии в журнал IEEE Transactions on Information Theory, но редакторам и рецензентам язык статьи показался слишком сложным. Лишь в 1983 году эта статья увидела свет в журнале ACM Newsletter Sigact News, и именно она стала первой в истории публикацией об основах квантовой криптографии.

Технологии История туалетной бумаги: самое деликатное изобретение

Первоначально Визнер и Беннет рассматривали вариант передачи зашифрованных сообщений с помощью квантовых «носителей», при этом подслушивание портило бы сообщение и не давало возможности его прочесть. Затем они пришли к улучшенному варианту — использованию квантовых каналов для передачи одноразовых «шифроблокнотов» — шифровальных ключей.

Закрытый конверт

Квантовые системы связи основаны на использовании квантовых свойств носителей информации. Если в обычных телекоммуникационных сетях данные кодируются в амплитуде и частоте излучения или электрических колебаний, то в квантовых — в амплитуде электромагнитного поля или в поляризации фотонов. Разумеется, потребуется значительно более дорогая и сложная аппаратура, но эти ухищрения оправданны: дело в том, что передача информации по квантовым каналам обеспечивает стопроцентную защиту от «прослушки». Согласно законам квантовой механики измерение свойств того или иного квантового объекта, например измерение поляризации фотона, неминуемо меняет его состояние. Получатель увидит, что состояние фотонов изменилось, и предотвратить это нельзя в принципе — таковы фундаментальные законы природы. Это можно описать такой аналогией: представьте себе, что вы пересылаете письмо в закрытом конверте. Если кто-то откроет письмо и прочитает его, цвет бумаги изменится, и получатель неминуемо поймет, что послание читал кто-то третий.

Самая ценная информация — это шифровальные ключи. Если ключ имеет длину, равную самому сообщению или еще длиннее, то расшифровать послание, не зная ключа, в принципе невозможно. Остается организовать защищенную передачу ключей, а это как раз и обеспечивают квантовые линии связи. Однако пока дистанция передачи данных для таких линий слишком коротка: из-за тепловых шумов, потерь, дефектов в оптоволокне фотоны не «выживают» на больших расстояниях.

Самая ценная информация — шифровальные ключи. Если ключ имеет длину, равную самому сообщению или еще длиннее, то расшифровать послание, не зная ключа, невозможно.

Криптография – квантовые ключи

Множество исследовательских групп по всему миру разрабатывают устройства «восстановления» квантовых данных — так называемые квантовые повторители, которые способны «оживлять» фотоны. Группа исследователей из Российского квантового центра под руководством профессора Александра Львовского нашла способ восстанавливать свойства фотонов и подтвердила в эксперименте работоспособность этого метода. Ученые занимались изучением феномена квантовой запутанности, при котором состояния двух или нескольких объектов — атомов, фотонов, ионов — оказываются связаны. Если состояние одного из пары запутанных фотонов измерить, то состояние второго немедленно станет определенным, причем состояния их обоих будут связаны однозначно — например, если один фотон окажется поляризован вертикально, то второй — горизонтально и наоборот.

«Если распределять пары запутанных фотонов между двумя удаленными партнерами, то они оба получают одну и ту же последовательность, которую можно использовать как шифровальный ключ, поскольку это истинно случайная последовательность, которую нельзя угадать или рассчитать. Если же кто-то попытается подсмотреть запутанные фотоны, корреляция между ними потеряется и из них больше нельзя будет извлечь ключ», — объясняет Александр Львовский.

Задача состоит в том, чтобы сохранить состояние квантовой запутанности при передаче на большие расстояния. До сих пор с этим возникали большие проблемы. По оптоволоконным сетям до сих пор не удавалось передавать запутанные фотоны на расстояние больше 100 км. На больших расстояниях квантовые данные просто теряются в шумах. В обычных телекоммуникационных сетях используют разные типы повторителей или усилителей сигнала, которые усиливают амплитуду сигнала и убирают шумы, но в случае с квантовыми данными этот подход не работает. Фотон нельзя «усилить», при попытке измерить его параметры состояние фотона изменится, а значит, все преимущества квантовой криптографии исчезают.

Квантовые повторители

Ученые из разных стран пытаются разработать технологию квантовых повторителей — устройств, способных «воссоздавать» квантовую информацию, не разрушая ее. Группа Львовского, кажется, нащупала путь, который может привести к успеху. Еще в 2002 году он и его коллеги обнаружили любопытный эффект, который был назван «квантовым катализом», по аналогии с химическим термином, где определенные реакции могут идти только в присутствии особого вещества — катализатора. В их эксперименте световой импульс смешивался со «вспомогательным» одиночным фотоном на частично пропускающем свет зеркале. Затем этот фотон «удаляли». Казалось бы, состояние светового импульса не должно было меняться. Но, в силу парадоксальных свойств квантовой интерференции, фотон менял его в сторону «усиления» квантовых свойств.

«В то время это явление выглядело не более чем курьезным феноменом, каковых в квантовой физике множество. Теперь же оказалось, что оно имеет важное практическое применение — позволяет восстановить запутанность квантовых состояний света», — говорит Александр Львовский.

В своей новой работе, отчет о которой был опубликован в журнале Nature Photonics, ученые научились заново запутывать «распутавшиеся» фотоны. В качестве источника запутанных фотонов в эксперименте они использовали нелинейный кристалл титанил-фосфата калия с периодической доменной структурой. Его «обстреливали» пикосекундными импульсами света, которые генерировал титан-сапфировый лазер. В результате в кристалле рождались запутанные пары фотонов, которые ученые отправляли в два разных оптических канала. В одном из них свет подвергался 20-кратному ослаблению с помощью затемненного стекла, в результате чего уровень запутанности падал почти до нуля. Это соответствует уровню потерь в 65 км обычного оптоволоконного кабеля. Затем ослабленный сигнал направляли на светоделитель, где и проходил процесс квантового катализа. Ученые из группы Львовского называют этот процесс «квантовой дистилляцией», поскольку на выходе остается меньше фотонов, зато их уровень запутанности возрастает почти до исходного. «Из миллиона слабо запутанных пар фотонов получается одна сильно запутанная. Но при этом уровень корреляции восстанавливается до первичной, и хотя скорость передачи данных несколько снижается, мы можем получить устойчивую связь на значительно большем расстоянии», — говорит коллега Львовского Александр Уланов.

Не только для шпионов

На основе этой технологии можно будет создавать квантовые повторители, пригодные для коммерческого использования. «Для этого есть и другие методы, но как их использовать в условиях существующих источников квантовой запутанности, непонятно. Это оказывается непропорционально дорого. Возможно, наш повторитель будет и проще, и дешевле», — говорит Львовский. По его мнению, при благоприятных условиях первый прототип такого повторителя может быть создан через четыре-пять лет. А появление его на рынке может открыть дорогу действительно массовому применению квантовой криптографии, что серьезно изменит жизнь не только военных или банкиров.

«Это касается каждого из нас. Квантовая криптография — это не только какие-то военные или шпионские секреты, это номера кредитных карточек, это истории болезни. У каждого из нас масса конфиденциальной информации, и чем более открытым становится мир, тем важнее для нас контролировать доступ к ней», — говорит Львовский. Использование квантовых методов передачи шифровальных ключей может серьезно ослож­нить жизнь злоумышленников, у которых теперь не будет возможности перехватить и расшифровать информацию.

Статья «Запутать распутанное» опубликована в журнале «Популярная механика» (№2, Февраль 2016). Интересно как устроен ядерный реактор и могут ли роботы построить дом?
Все о новых технологиях и изобретениях!ОКЯ соглашаюсь с правилами сайта Спасибо.Мы отправили на ваш email письмо с подтверждением.Ещё больше по темам

Источники:

• https://www.krugosvet.ru/enc/kriptografiya
• https://naked-science.ru/article/sci/sovremennaya-kriptografiya-zaboty
• http://www.tadviser.ru/index.php/%D0%A1%D1%82%D0%B0%D1%82%D1%8C%D1%8F:%D0%9A%D1%80%D0%B8%D0%BF%D1%82%D0%BE%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D1%8F
• https://www.PopMech.ru/technologies/235655-kvantovaya-kriptografiya-chto-eto-takoe/